I've often wondered at the links between mathematics and philosophy. I mean, historically, it's clearly been quite close. Major mathematicians we accredit with much of the development of maths as we know it today, are the exact same people we accredit as being the big thinkers in philosophy. Descartes being a HUGELY obvious one! But then there's also Pythagoras - not known quite so much for his philosophies, mainly because they didn't carry over much to modern-day. Nor did many people even agree with him in his own time. But he was SUCH an interesting man - who all most people know about him came from his theorem on triangles.
I don't know if anyone's been watching 'Atlantis' on BBC, and I know the reviews aren't great - but I really like it! It's a bit of fun - you don't have to think too seriously when you're watching it; which is nice once in a while! Anyway, I think the Pythagoras character on there is lovely, he's the sort of guy everyone would like! Which is great for uplifting mathematics, and geekiness, and cleverness; and quirkiness I guess!
The context in which I got re-excited about him this time, was in reading Fear and Trembling by Kierkegaard, the great Danish philosopher. He assimilates the paradox of faith making inwardness better than outwardness, to Pythagoras' belief that odd numbers are better than even numbers. Now, if you've read my post about the number 86, you will know that I MUCH prefer odd numbers to even ones! So to discover this little nugget of useless information, was SO exciting!!!
But now I want to tell you a story. Because I love telling this story. As far as I'm aware it's a true story - though I couldn't point you in the direction of any evidence. It's a story about Pythagoras.
Now, Pythagoras believed that numbers were whole and pure and that they could always be expressed as a relationship between two whole numbers. So for example, if you had a line 2.5 units long, you could just make the units 1/2 the size and say it was 5 units long. And he thought this could always be the case.
So then he came up with his awesome triangle theorem, which was that the square of each of the legs of a right-angle triangle summed to the square of the hypotenuse. Not the number squared as we would have it today, because that didn't exist yet, but the actual shape of a square. And he believed this would always be the case and the side would always be a whole number you just had to work out what size to divide the units to be.
The problem came with a triangle of leg-length 1. One of Pythagoras' followers (he had a cult which only certain people were allowed to join) then showed, using Pythagoras' own theorem, how the resulting length of the hypotenuse couldn't possibly be a whole number, nor ever expressed as one. A simple way to prove this is to think about odd and even numbers. If the sum of the square of the two legs of the triangle have to add together to give the square of hypotenuse, then if the hypotenuse was a whole number, the square of the hypotenuse would have to be even, to be able to split equally between the two legs. But if that square is even (so is the hypotenuse because an even x even = an even) then so must be half of that square and therefore so must each of the legs. But 1 is not even, so this whole situation cannot exist with just whole numbers.
Pythagoras didn't like this, so told that follower who had come up with it not to tell anyone. Eventually, the follower came clean and told of his great proof, and so Pythagoras took him out into the sea and threw him overboard to die.
This is the story of how Pythagoras was not only a mathematician, not only a philosopher, but also... A MURDERER!
If you haven't seen it, I would really recommend watching the following video from Vihart!
http://www.youtube.com/watch?v=X1E7I7_r3Cw
It's really good and as more of the story on than I have shared here! It also shows the same proof that I have used above and is - as all of Viharts stuff is - AMAZING MATHY FUN TO WATCH!!! :D
Confessions of a Secret Mathematician
Friday, 20 December 2013
Sunday, 10 November 2013
Archimedean AND Logarithmic Spiralling!!!

I was at a meal this evening with a Mathmo from Trinity - he was really lovely, and definitely stereotypically a Mathmo!!! We had a GREAT time! It was a meal with a family from church; because we're freshers and new to the area, it's really nice to be in a family environment sometimes! Anyway, so they had circular table mats a bit like (not exactly but I felt it would be slightly frowned upon to take out my phone to take a picture of their table mats during dinner) the picture above. And me and this mathmo suddenly decided it would be normal - having said that, who wants to be "normal" anyway?! - to determine what kind of spiral the pattern on the mats was making.
Now you can see that it is an Archimedean spiral. It spirals out from the centre such that each "strand" is the thickness and each would reach the same radius line (if you drew it on) the same width from the last one as the next one does. I mean, if you want to be REALLY technical, the above illustration doesn't show this as well as the ones at dinner because the individual strands in the ones at dinner seemed more twisted themselves and so the whole thing was tighter - whereas this one looks tighter in the centre than it does as this spreads out. I think it's a different kind of weaving; but still the best example I could find!
Now if you look up what an Archimedean spiral is, you will soon come across it contrasted against a logarithmic spiral. This is because whereas an Archimedean spiral reaches a radius line at equally spaced intervals; with a logarithmic curve, the spacing of this gets wider and wider as the spiral goes on. So how, I hear you ask, can it be both?!
Well... If you actually tried to trace your finger round the spiral, following the path of least resistance or just in a way that meant you allowed the pattern to guide where your finger was going, you quickly found that your finger was actually spiralling out much more like a logarithmic curve than like the Archimedean curve you expect from looking at it.
Which is REALLY cool. I mean, who doesn't like surprises?!
The reason for this is because, for any point in the spiral, if you drew a line from the radius out to that point, and then another line showing the gradient of the spiral at that point, the angle between those two lines would be constant all the way round the circle.
Now this is VERY unlikely to have been an intentional design idea but more likely to be just an effect of the tightness in which the strand of wicker had been twisted - but all the same it's a pretty awesome conversation starter at the dinner table!!! Me and this Trinity Mathmo managed to get EVERYONE holding up their place mat tracing round the spiral. A great bit of interactive maths which not only highlights the difference between an Archimedian spiral and a logarithmic spiral - but also shows that sometimes, actually discovering/doing/finding out for ourselves, is so much more powerful than just looking at something - or as a teacher, just showing something - and expecting to grasp it completely in all it's beauty and fullness!
After meeting the lovely family I shared the meal with, this was definitely one of the major highlights of today!!! :D
Friday, 8 November 2013
Rediscovering Integration!!!
In order to keep up my maths and leave my options for next year as open as possible, I’ve been teaching myself the modules for Further Maths A-Level. So far, it’s going really well and I’m doing 1 module per month, meaning I should have completed all 6 by the end of February and can focus on past papers from that point until the exams at the end of May/throughout June (it’s a sad thing there are no January exams any more!).
Anyway, having done Decision D1 (in my mind, not mathematics, but helpful for anyone wanting to go into computer science of logic) and Mechanics M1 as my applied modules last year, I had to discover Statistics for the first time this year!
Now Stats was always going to have a hard act to follow, as I absolutely ADORED mechanics! My mechanics revision is what you will see written all over the window both still in the Maths Workroom of my school last year, and also as my cover photo if you wander over to my Google+ Profile Page (+María Norlov)! I LOVED it. It was just so much fun. So then Stats… well, I’m sorry statisticians, but it just doesn’t have the same draw for me. I mean, FP01 has by far been the best module I’ve done so far and I am definitely more interested in Number Theory type questions than applied mathematics, but Stats just isn’t so fun even within that bracket.
Or that was until (dun dun duuuuuuuuun) we reached Chapter 3 of S2 and we hit integration!!! I was like, what on earth is integration doing here? Turns out continuous random variables give us probability density functions and cumulative distribution functions which give us a graph, the area under which, of course, equals 1 (as it is probability), but also gives us the opportunity to integrate to obtain the area for specific sections, or to integrate and equal to one to find any constants we don’t yet know. And it all go me to thinking; ‘What actually IS integration? How does it work?!’
| Right, Left, Maximum and Minimum methods for calculating Riemann sums as shown in the link below! |
I mean, we integrate an equation of a line between two points and it gives us the area under the curve. So I thought back to when I was first introduced to integration, and sadly - I think now - I believe it was just as a “Fundamental Theorem of Calculus”. Just as the opposite to differentiation really. Which is sad, considering it is actually such a beautiful mathematical phenomenon. Integration gives us the area under the curve, right? Well this is because it is like splitting the area under the curve into infinitely many and infinitely small strips which we can then find the area of and add to get the area under the entire curve. That’s why we integrate ‘with respect to x’ or ‘dx’. Imagine ‘dx’ as relating to ‘x’ meaning a ‘small part ofx’. And this is a small part of x where the width of this strip is getting infinitesimally close to 0.
And then just think about that! How amazing is integration?!?!?! That it can contain within it infinitely many strips to get an accurate estimate for the area under the curve! The coloured picture above actually shows estimates made by various ways of calculating ‘Riemann sums’ [another wonderful thing that came from the world of Bernhard Riemann - his famous hypothesis is one of the things that inspired me to a love of mathematics in the first place!!!]. And it shows how these converge to give closer and closer to the right answer, obviously, the more strips the space is divided into. But if you look at all the complexity that goes into Riemann sums (http://en.wikipedia.org/wiki/Riemann_sum), you will very quickly begin to see that the relative simplicity and beauty (and contained-ness if I might push the limits of English vocabulary!) of the humble integration. I mean, can you IMAGINE having to calculate Riemann sums every time you wanted the area under a curve?!?!?! And apparently it is defined by being merely the opposite of differentiation.
And then just think about that! How amazing is integration?!?!?! That it can contain within it infinitely many strips to get an accurate estimate for the area under the curve! The coloured picture above actually shows estimates made by various ways of calculating ‘Riemann sums’ [another wonderful thing that came from the world of Bernhard Riemann - his famous hypothesis is one of the things that inspired me to a love of mathematics in the first place!!!]. And it shows how these converge to give closer and closer to the right answer, obviously, the more strips the space is divided into. But if you look at all the complexity that goes into Riemann sums (http://en.wikipedia.org/wiki/Riemann_sum), you will very quickly begin to see that the relative simplicity and beauty (and contained-ness if I might push the limits of English vocabulary!) of the humble integration. I mean, can you IMAGINE having to calculate Riemann sums every time you wanted the area under a curve?!?!?! And apparently it is defined by being merely the opposite of differentiation.
I encourage you, see integration for what it is today - it’s not merely the undoing of differential equations, it is something all of itself which contains within it the mystery of infinity. And that shouldn’t be something that is over-looked! Having not used integration for a while, I forgot how immensely wonderful it is; thankfully, today I rediscovered it! :D
Friday, 1 November 2013
Little Addition to my Tribute to Pi!!!
I've just realised. I never actually explained what I meant in the title of my last post when I called Tau ‘adolescent’! It is merely that from my point of view, it looks as though Pi is the legend - is the genius and the well-known star from history, and Tau is coming in as though it’s the new teenager ready to show off what it’s all about. It just has that “typical teen” characteristic of needing to PROVE it’s great. Whereas Pi doesn’t need to prove it’s great, that comes with the territory of being Pi. Obviously, I realise this anthropomorphism of numbers has a way of possibly going too far, but then, they do seem to have their own personalities sometimes!
I also just wanted to share a really cool photo! For a while, before I came to uni, I had a Saturday job working at a beautiful little Tea-Room in my home village - not that I was very good at my job, but the people that I met there were all great! Anyway, one day Saturday morning, it was quiet and so I was learning to make a pie from the chef and she had a bit of leftover pastry at the end, so I said she should definitely make a picture out of it to put on the top. Then I had a brainwave! If she put the symbol for Pi on the top, it would be a Pi pie!!! And, amazingly, that’s exactly what she did - just for me! To my utter delight; I spent the rest of the day showing everyone who came in the Pi pie and we sold all of it!

BEAUTIFUL!!!
I also just wanted to share a really cool photo! For a while, before I came to uni, I had a Saturday job working at a beautiful little Tea-Room in my home village - not that I was very good at my job, but the people that I met there were all great! Anyway, one day Saturday morning, it was quiet and so I was learning to make a pie from the chef and she had a bit of leftover pastry at the end, so I said she should definitely make a picture out of it to put on the top. Then I had a brainwave! If she put the symbol for Pi on the top, it would be a Pi pie!!! And, amazingly, that’s exactly what she did - just for me! To my utter delight; I spent the rest of the day showing everyone who came in the Pi pie and we sold all of it!
BEAUTIFUL!!!
Thursday, 31 October 2013
The Beauty of Pi; the Adolescence of Tau; and the Occasional Disharmony Between the Two
I happened across an article today - it was the 'Theorem of the Day' I saw in a Google+ post. It was about Machin's formula; which, from every other source I have ever seen, is usually expressed as:
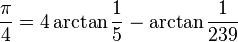
It wasn't just this that I found slightly bizarre (by the way the bizarreness is not in the difference in how each presents arctan), but throughout the article they kept then referring to different ways of estimating Pi - ways that had been used in the history of mathematics - but calling it Tau/2. This is just so strange!!! I then noticed the "Tau Manifesto Compliant" logo in the bottom corner, but I just don't get why anyone would go this far!
I mean, I'm a fan of Greek letters - to the point where I've learnt a bit of koine Greek and so on - and I do like Tau. I think when you're using "2Pi" a lot, it is possibly easier (especially for coding) to have "Tau=2Pi" at the top and use tau from there in. But not at the expense of Pi! Not to keep using "Tau/2" - it's nonsensical!
I think what is lost here is the beauty of what Pi is - and has been - throughout mathematical history. It is not that we want to sanctimoniously hold on to Pi as if it has some intrinsic value - but rather that it is a beautiful constant which epitomises perfectly the direct harmony between order (the constant and necessary nature of Pi) in the natural world and chaos (the random and never repeating nature of the number itself) in the only way we can interpret it.
Which all reminded me of an ABSOLUTELY beautiful expansion - the Taylor series:

And how this can be manipulated to give:
Which is just beautiful.
Not only does it give us a function and way of estimating Pi (although for this purpose alone it is not the best one and there are many others which converge MUCH quicker than this one does!!!), it also uses the odd numbers as the denominators (and powers, though with 1 this is irrelevant) - which if you've read my last post, you'll know I like! ;)
Nowadays, with our calculators that use Pi accurately and extensively, and computers which can generate Pi to any necessary number of digits, there is little need for exploration into this kind of systematic beauty that pi has always been a source of in mathematics.
The fact alone that the circumference of any circle will be Pi multiplied the diameter is astoundingly explanatory of what a circle is - a shape of which you could never reach the full extent of defining exhaustively. Just as the digits of Pi go on forever with no end, so do the intricacies of the natural world and even the humble circle.
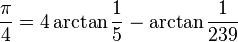
However, on this particular website, it was expressed as:
It wasn't just this that I found slightly bizarre (by the way the bizarreness is not in the difference in how each presents arctan), but throughout the article they kept then referring to different ways of estimating Pi - ways that had been used in the history of mathematics - but calling it Tau/2. This is just so strange!!! I then noticed the "Tau Manifesto Compliant" logo in the bottom corner, but I just don't get why anyone would go this far!
I mean, I'm a fan of Greek letters - to the point where I've learnt a bit of koine Greek and so on - and I do like Tau. I think when you're using "2Pi" a lot, it is possibly easier (especially for coding) to have "Tau=2Pi" at the top and use tau from there in. But not at the expense of Pi! Not to keep using "Tau/2" - it's nonsensical!
I think what is lost here is the beauty of what Pi is - and has been - throughout mathematical history. It is not that we want to sanctimoniously hold on to Pi as if it has some intrinsic value - but rather that it is a beautiful constant which epitomises perfectly the direct harmony between order (the constant and necessary nature of Pi) in the natural world and chaos (the random and never repeating nature of the number itself) in the only way we can interpret it.
Which all reminded me of an ABSOLUTELY beautiful expansion - the Taylor series:

And how this can be manipulated to give:
Which is just beautiful.
Not only does it give us a function and way of estimating Pi (although for this purpose alone it is not the best one and there are many others which converge MUCH quicker than this one does!!!), it also uses the odd numbers as the denominators (and powers, though with 1 this is irrelevant) - which if you've read my last post, you'll know I like! ;)
 |
Pi to 10,000 decimal places by Christian Ilies Vasile. Imagine a
string going from one digit on to the next: 3, 1, 4, 1, 5, 9, 2... and
changing colour each time it hit a different digit!!!
|
The fact alone that the circumference of any circle will be Pi multiplied the diameter is astoundingly explanatory of what a circle is - a shape of which you could never reach the full extent of defining exhaustively. Just as the digits of Pi go on forever with no end, so do the intricacies of the natural world and even the humble circle.
Friday, 25 October 2013
The Number 86
Now, it is particularly odd for me to be writing ANYTHING titled to be about the number 86. I mean, 86?! Of all numbers...
Something, admittedly, strange about me when it comes to numbers, is that generally, I don't like even numbers. I'm not sure what it is, but I just don't like them. I like odd numbers. I think I will always have a group of many, changing, favourite numbers (which we can explore in due course) but as the favourite of all my favourite numbers it will be the number 1. That is why my profile picture is a number 1. 1 is so simple. So lovely. 1 is, as the first positive odd number, almost more odd than any other number! And though other "favourite numbers" can be favourite for this cool reason or that, there will always be another number with another cool reason to be a favourite number - whereas there will never be another number to start off the whole counting system!
So anyway, it is strange that I would be writing about the number 86 - it is even, contains only even digits, and it's not even part of many of the categories which make up lots of my favourite numbers. It's clearly not prime (by far the best grouping of numbers!!! > which brings me on to the mixed feelings I have for the number 2 - it's like the most even of even numbers - using the same logic as for 1 being the most odd of odd numbers - and yet it is also prime; what are you supposed to do with that kind of situation?!), it's not a smith number, nor a perfect number, it's not a primary pseudo-perfect number, it's not a harshad number, it's not narcissistic, or amicable, and there are many other things which the number 86 is not. So why then, write a post about the number 86???
Well, when I arrived at Cambridge University - well about half a week later when I'd finally worked out how the intranet worked here - I had been issued with an email address of the form ...@cam.ac.uk. But it doesn't stop there, this ... section of the address is also my log in for every single possible website, computer or ANYTHING to do with my time here in Cambridge at all. And part of this, featured the number 86 - to my utter disdain when I found this out.
Eventually, after trying all of the number types above (and many more) to find 86 is none of those either :( I was almost at the point of leaving the university altogether {DISCLAIMER: that may be a slight exaggeration}. So I paid a visit to the Zoo (the Zoo of Numbers, that is)!!! And this is a pretty good website - it has interesting facts (some not mathematical) about practically every single number you could possibly require an interesting fact for! And here, I discoverd that 86 is a happy number!
Now happy numbers were something I vaguely remembered having seen a +Numberphile video on ages ago - so I looked this up. Happy numbers are numbers that if you square each digit and then add them together, and repeat this to that answer and so on, you eventually reach the number 1 (told you the number 1 is great)! So, turns out, 86 is actually VERY happy as it only takes 2 iterations to reach 1:
You might be wondering what happens if it does not go back to 1. What happens with all the "unhappy" numbers [by the way, don't ask me why they're called happy/unhappy numbers - it has to be one of the soppiest namings of all time!!!]? Well, they all (when squaring the numbers and operating in base 10) go back to the same cycle and would just go round and round forever. This can be shown in my beautiful drawing to the right:
A fitting name for this cycle, I feel, was that of the "melancoil" as named by Matt Parker in the Numberphile video on that! In my diagram, the cycle starts with 16 (circled) and goes like this:
Something, admittedly, strange about me when it comes to numbers, is that generally, I don't like even numbers. I'm not sure what it is, but I just don't like them. I like odd numbers. I think I will always have a group of many, changing, favourite numbers (which we can explore in due course) but as the favourite of all my favourite numbers it will be the number 1. That is why my profile picture is a number 1. 1 is so simple. So lovely. 1 is, as the first positive odd number, almost more odd than any other number! And though other "favourite numbers" can be favourite for this cool reason or that, there will always be another number with another cool reason to be a favourite number - whereas there will never be another number to start off the whole counting system!
So anyway, it is strange that I would be writing about the number 86 - it is even, contains only even digits, and it's not even part of many of the categories which make up lots of my favourite numbers. It's clearly not prime (by far the best grouping of numbers!!! > which brings me on to the mixed feelings I have for the number 2 - it's like the most even of even numbers - using the same logic as for 1 being the most odd of odd numbers - and yet it is also prime; what are you supposed to do with that kind of situation?!), it's not a smith number, nor a perfect number, it's not a primary pseudo-perfect number, it's not a harshad number, it's not narcissistic, or amicable, and there are many other things which the number 86 is not. So why then, write a post about the number 86???
Well, when I arrived at Cambridge University - well about half a week later when I'd finally worked out how the intranet worked here - I had been issued with an email address of the form ...@cam.ac.uk. But it doesn't stop there, this ... section of the address is also my log in for every single possible website, computer or ANYTHING to do with my time here in Cambridge at all. And part of this, featured the number 86 - to my utter disdain when I found this out.
Eventually, after trying all of the number types above (and many more) to find 86 is none of those either :( I was almost at the point of leaving the university altogether {DISCLAIMER: that may be a slight exaggeration}. So I paid a visit to the Zoo (the Zoo of Numbers, that is)!!! And this is a pretty good website - it has interesting facts (some not mathematical) about practically every single number you could possibly require an interesting fact for! And here, I discoverd that 86 is a happy number!
Now happy numbers were something I vaguely remembered having seen a +Numberphile video on ages ago - so I looked this up. Happy numbers are numbers that if you square each digit and then add them together, and repeat this to that answer and so on, you eventually reach the number 1 (told you the number 1 is great)! So, turns out, 86 is actually VERY happy as it only takes 2 iterations to reach 1:
86: 8^2 + 6^2 = 64 + 36 = 100
100: 1^2 + 0^2 + 0^2 = 1 + 0 + 0 = 1
So I thought, well that's great! But to be honest, it's probably not that rare - and numbers have much better reasons for being good when those reasons make them rare! So I set about working out, for all the numbers up to 100, how many were happy. I found that, surprisingly, only 20 numbers from 1 - 100 (including both 1 and 100) are happy numbers. That's 1 in 5 - and my 86 happened to be a part of that! Things were starting to look up for my relationship with my ID.
 |
| The happy numbers are in the boxes at the top; the other numbers all feed into the red circle in the middle! [16, 37, 58, 89, 145, 42, 20, 4, 16...] |
A fitting name for this cycle, I feel, was that of the "melancoil" as named by Matt Parker in the Numberphile video on that! In my diagram, the cycle starts with 16 (circled) and goes like this:
16: 1^2 + 6^2 = 1 + 36 = 37
37: 3^2 + 7^2 = 9 + 49 = 58
58: 5^2 + 8^2 = 25 + 64 = 89
89: 8^2 + 9^2 = 64 + 81 = 145
145: 1^2 + 4^2 + 5^2 = 1 + 16 + 25 = 42
42: 4^2 + 2^2 = 16 + 4 = 20
20: 2^2 + 0^2 = 4 + 0 = 4
4: 4^2 = 16
and there is starts again!
So if any number, at any point in doing this to it, contains one of these 8 numbers; it will feed into this cycle. And when using the power of 2 and working in base 10, these are the ONLY 2 possibilities - it either feeds down to 1 or it gets trapped in this cycle. That's pretty cool. As far as mathematical importance goes, it's considered "recreational number theory"; but hey, it's made my identification at uni bearable - so I'll say it's pretty important right now!!!
But it does make you wonder... Why does this happen? Where could it lead? If anyone knows of any mathematical research articles or anything on these numbers I would be interested to find out - I conducted a brief search of the web and only found the Wikipedia page. It would be odd if NO-ONE thought to just see where it takes them!!!
This is why I love number theory - sometimes, it can just be so abstract and unrelated to the real world that it makes you stand back and just appreciate it. It stops your mind from running a hundred miles a minute just trying to keep up with all the practicalities of life - with this, you just experience and discover; in your own time how you like to. It's nice to do something without an agenda sometimes!!!
Wednesday, 23 October 2013
OK... So the Background!
Hi. My name is María Norlov and I am confessing to be a secret mathematician.
You might be a little confused about what this is; but I promise you, all will soon become clear. I am a first year student at the University of Cambridge, Enlgand. My Mother is Spanish and my Father is Danish (although that's more an insight into where my name comes from than anything else), but we have lived here in the UK for about 7 years now! My confession is that I love maths - like genuinely, actually adore it. >ooops; anyone who thought I was cool before, now really doesn't!!! {Oh, and before I get going; I apologise but this is probably going to be a REALLY long post - hopefully once all the background is covered they will be more concise and fun!}
Anyway, the reason I have to be a secret mathematician is because it is safe to say that I am definitely not studying maths.
I only realised this passion for numbers and mathematics that I have in my final year of A-levels. I went to a state school (not many of those here in Cambridge no matter what they say about diversity) - and to add to that; a Northern state school (even less of those here) - and up until A-level I had pretty much just breezed through everything with barely any real effort or work. I mean, I enjoyed my school work - I always finished the work in class and asked for the extension, I always did my homework, I always revised before tests; but it never really needed a noticeable amount of my time or effort. I was lucky.
When I got to A-levels, I suddenly realised that I could direct my work where I wanted; although less so in year 12 than in year 13. In year 12, not wanting to close any doors, I did eight AS' (the usual is 4 or 5), which I admit didn't leave me with much time to spare. Again, I enjoyed my studies but it was all still very much just learning to the exam - which I kind of always saw as pointless. But, by the end of year 12 I had certainly discovered a love of learning. I wanted knowledge, understanding, skills, etc. I loved to learn.
It was at this point which I had to choose what subject I wanted to apply for at university. I looked at what A-levels I really enjoyed and wanted to know more about and I chose one which I was particularly interested in to pursue further. Eventually deciding on this as my degree choice when applying. By the October (1 month into being in year 13), the deed had been sealed; I had chosen the all-important path for my life to follow from that point on.
Or at least that's how it's made to feel. All this pressure - you suddenly have to make a decision which you not only can't possibly know how you will feel about when you actually get to it, but also one that will apparently retain so much importance for the next 3 years at least; and quite probably beyond.
As for mathematics at this point, even throughout year 12 - although a change was beginning to arise - maths had always just been something I was good at. Something I did. And quite frankly, I was more interested in what I knew and wanted to know than what I could merely do.
There are two main problems in how mathematics is taught throughout school as far as I can see:
You might be a little confused about what this is; but I promise you, all will soon become clear. I am a first year student at the University of Cambridge, Enlgand. My Mother is Spanish and my Father is Danish (although that's more an insight into where my name comes from than anything else), but we have lived here in the UK for about 7 years now! My confession is that I love maths - like genuinely, actually adore it. >ooops; anyone who thought I was cool before, now really doesn't!!! {Oh, and before I get going; I apologise but this is probably going to be a REALLY long post - hopefully once all the background is covered they will be more concise and fun!}
Anyway, the reason I have to be a secret mathematician is because it is safe to say that I am definitely not studying maths.
I only realised this passion for numbers and mathematics that I have in my final year of A-levels. I went to a state school (not many of those here in Cambridge no matter what they say about diversity) - and to add to that; a Northern state school (even less of those here) - and up until A-level I had pretty much just breezed through everything with barely any real effort or work. I mean, I enjoyed my school work - I always finished the work in class and asked for the extension, I always did my homework, I always revised before tests; but it never really needed a noticeable amount of my time or effort. I was lucky.
When I got to A-levels, I suddenly realised that I could direct my work where I wanted; although less so in year 12 than in year 13. In year 12, not wanting to close any doors, I did eight AS' (the usual is 4 or 5), which I admit didn't leave me with much time to spare. Again, I enjoyed my studies but it was all still very much just learning to the exam - which I kind of always saw as pointless. But, by the end of year 12 I had certainly discovered a love of learning. I wanted knowledge, understanding, skills, etc. I loved to learn.
It was at this point which I had to choose what subject I wanted to apply for at university. I looked at what A-levels I really enjoyed and wanted to know more about and I chose one which I was particularly interested in to pursue further. Eventually deciding on this as my degree choice when applying. By the October (1 month into being in year 13), the deed had been sealed; I had chosen the all-important path for my life to follow from that point on.
Or at least that's how it's made to feel. All this pressure - you suddenly have to make a decision which you not only can't possibly know how you will feel about when you actually get to it, but also one that will apparently retain so much importance for the next 3 years at least; and quite probably beyond.
As for mathematics at this point, even throughout year 12 - although a change was beginning to arise - maths had always just been something I was good at. Something I did. And quite frankly, I was more interested in what I knew and wanted to know than what I could merely do.
There are two main problems in how mathematics is taught throughout school as far as I can see:
- It is the thing that no one wants to love; and
- The only way teachers try and make students love it is through showing them what it's practically good for
Now, on this second point; it is not that the practical application of mathematics isn't important. And indeed, it is this application which will enable the huge numbers of Nat-Sci's to continue to fill this university and others like it [Nat-Sci's are Natural Sciences students and there are SOOO many here right now!]. But my problem with it is that this shouldn't be the ONLY way that people are shown to love it.
In year 13, I was suddenly working with a much more beautiful and knowledge based form of maths. I was no longer just learning rules and putting them into practice - which although I have always loved for it's therapeutic nature, it never quite spurred a passion within that this was something amazing! Now, I had to bring all the rules I had learnt before and actually make new things happen with it. I had to know, I had to understand and I had to create. These three things brought something more to maths than just simply doing. It was this "more" which I needed and strived for.
Having not studied the correct formal qualifications to get into the top universities to do maths, even with my 3 A*'s at A-Level, nowhere would accept me. So I resigned to the idea of, having already made my bed, simply lying in it.
Though I must point out; it's not as if I do not enjoy my subject. I thought when I got into university, I would soon fall head-over-heels in love with learning all this new knowledge, that it wouldn't even matter to me what the subject was. But so far, it's killing me not being able to tell anyone how much I love maths - hence this blog. My daily dose of Further Mathematics A-level gets me through the day at the moment - with my own subject not holding that same need for proof in understanding nor that ability to create for which maths became my passion.
I don't know where I will end up in the future; or where I even want to! But right now, that doesn't matter - what matters is that I've got someone to share my mathematical insights, confusions, joys and amazements with: you!
Subscribe to:
Posts (Atom)